Gray code
Gray code, also known as reflected binary code, is a code having digits 0 and 1. Gray code do not have place value for its digits. Any successive codes in Gray code system have only one bit changes.
Decimal Number
Whole number, a decimal point and a fractional value combines to form a decimal number. The decimal point separates the whole number part from the fractional part of the number. Each digit of a decimal number can be any number from 0 to 9. Any value less than 1 is written to the right of decimal point. Decimal numbers are also known as base-10 number or counting numbers. Place value of decimal number varies as the whole number powers of 10 starting from the left of decimal point. Similarly, the place value of digits left to decimal point varies as the division of power of tens.
Binary number
Binary numbering system uses only two symbols 0 and 1. Each digits of a binary number is referred to as bits. Binary system is also known as base -2 system. Each digit is represented by the increasing power of 2 from the LSB (Least Significant Bit). Binary system is the heart of digital electronics and is used for information flow. In digital electronics, 0 and 1 are used to denote logic states, high and low. Arithmetic operations are also possible in binary system.
Gray code to decimal conversion
Gray code cannot be directly converted to decimal. For converting gray code to decimal, we have to convert the gray code to binary first and then convert the binary code to decimal.
Gray to decimal conversion can be well understood with an example.
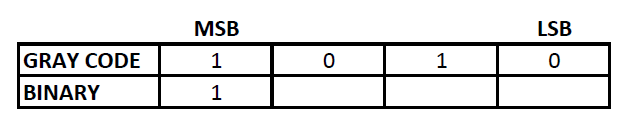
Let us convert 1010 from gray code to decimal value:
To convert 1010 to decimal, we have to convert 1010 to binary first.
Step 1: The MSB (Most Significant Bit) of a binary and gray code will be the same.
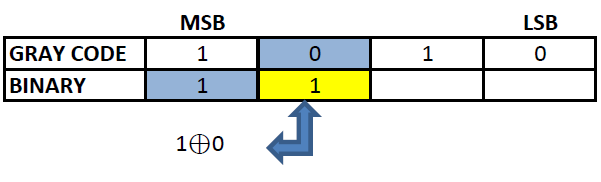
Step 2: The next digit of binary will be the EXOR of the MSB of binary and the second MSB of the gray code.
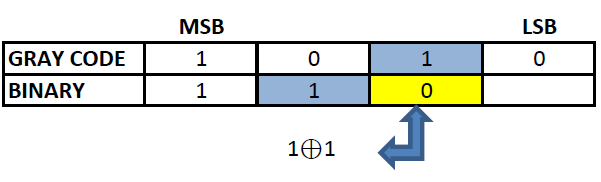
Step 3: Similarly EXOR the digit obtained in the previous step and the third MSB of gray code to obtain the third MSB of binary.
Step 4: Repeat the previous step till the LSB of gray code is found.
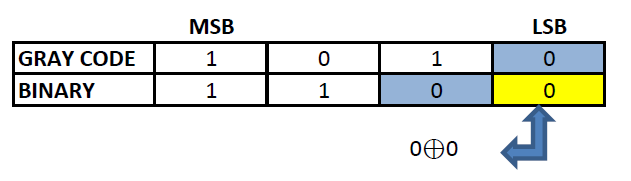
The Binary corresponding to gray code 1010 is 1100. Now this binary code can be converted to decimal.
Binary number can be converted into decimal number using the following formula:
Decimal Number = (Dn X 2n + …………… + D2 X 22 + D1 X 21 + D0 X 20).
Where,
Dn – D0 → digits of a binary number.
n → Position count starting from 0 (left to right).
Applying the above formula,
Decimal Number = 1 x 23 + 1 x 22 + 0 x 21 + 0 x 20 = 8 + 4 =12
Therefore, Gray code 1010 = 1210

Good