Decimal Number
Whole number, a decimal point and a fractional value combines to form a decimal number. The decimal point separates the whole number part from the fractional part of the number. Each digit of a decimal number can be any number from 0 to 9. Any value less than 1 is written to the right of decimal point. Decimal numbers are also known as base-10 number or counting numbers. Place value of decimal number varies as the whole number powers of 10 starting from the left of decimal point. Similarly, the place value of digits left to decimal point varies as the division of power of tens.
Hexadecimal Number
Hexadecimal number system uses 16 different symbols to represent a numeric value. It uses numbers 0 to 9 and alphabets A to F for representation. . The place value of each digits of an hexadecimal number varies as the whole number powers of 16 starting from the right (Least Significant Digit). The first single digit number in hexadecimal system is 0 and the last is F. Similarly, the first two digit hexadecimal number is 10 and the last is FF and so on. It is used as an alternative for binary numbers by developers and programmers.
How to convert decimal to hexadecimal:
To convert any decimal number to hexadecimal follow the below steps:
Step 1:
Divide the number by 16 and note down the quotient and reminder. Let it be reminder-1 and quotient-1 respectively.
Step 2:
Again divide the quotient-1 by 16 and note down the quotient and remainder as reminder-2 and quotient-2.
Step 3:
Repeat Step-1 and Step-2 until the quotient becomes zero.
Step 4:
If the reminder is greater than 9, replace it with the alphabet from following table:
| 10 | A |
| 11 | B |
| 12 | C |
| 13 | D |
| 14 | E |
| 15 | F |
Step 5:
Assume you have done the division ‘n’ times until you got a quotient of 0. From the first reminder, write down all the reminders from right to left.
Use Decimal to Hexadecimal convertor
Example for Decimal number to hexadecimal conversion
Example-1
Convert 98110 to hexadecimal
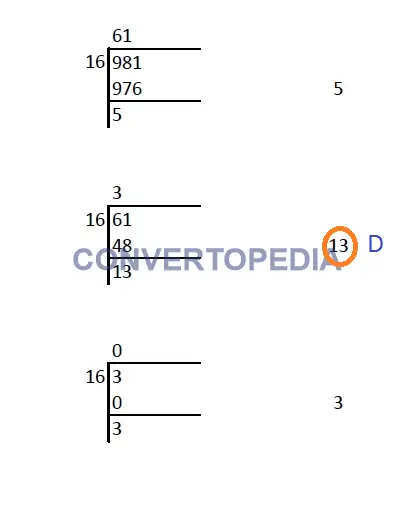
Hence, 98110 = 3D516
Example-2
Convert 466510 to hexadecimal
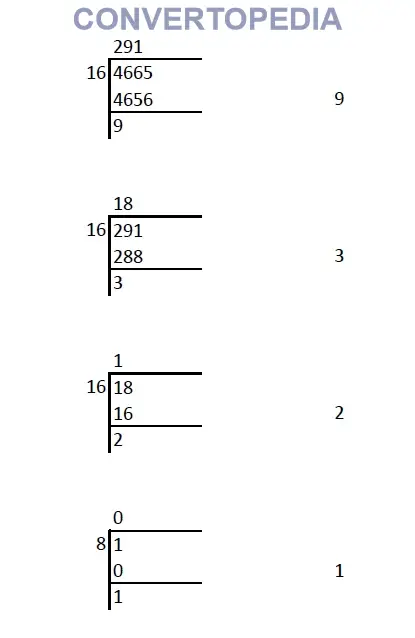
Hence, 466510 = 123916